Class 10th Maths Solution in Hindi Bihar

Class 10th Maths Solution in Hindi Bihar and UP

Class 10th Maths Solution in Hindi : Mathematics is one of the most important subjects which can be applied in our daily life. No matter what your dream job is, whether you want to be a Pilot, Engineer, Doctor, or Professor, mathematics is always required.

नीचे दिए गए वीडियो पर क्लिक करके देख सकते हैं।

I believe it is one of the most interesting subjects. When I was a student I use to enjoy dealing with mathematics since there is nothing that I have to remember apart from some few formulas. Here I will discuss the topic of Class 10th Maths Solution in Hindi in detail.

 

Today we will be learning about some of the basic topics of mathematics which is going to help you in your studies. The topics that are going to be discussed are too easy to understand and it can help you have a proper foundation of mathematics.

यहाँ हम दशवी गणित को एक एक करके सीखेंगे।  लिंक निचे है इसके माध्यम से पढ़  सकत है |

चैप्टर वाइज लिंक है इसे जरूर फॉलो करे

Real Number   (वास्तविक संख्या)

Polynomials   ( बहुपद )

Pair of linear equations in two variables  (दो चार वाले रैखिक समीकरण युग्म )

Quadratic Equations   (द्विघात समीकरण )

Arithmetic Progression (समान्तर श्रेढ़ी )

Triangles    (त्रिभुज )

Co-ordinate Geometry   (निर्देशांक ज्यामिति )

Trigonometric ratio and identities (त्रिकोणमिति का परिचय )

Circle    ( वृत )

Areas related to circle     (वृत  सम्बंधित क्षेत्रफल )

Construction   (रचनाए )

Surface areas and volume  (पृष्ठीय क्षेत्रफल और आयतन )

Statistics  (सांख्यिकी )

Probability  (प्रायिकता )

*****************************************

**** Also Read  ****

—–– Social Science & Science CLASS 10TH

—— GK -QUIZ IN HINDI

—— (NATIONAL & INTERNATIONAL ) IMPORTANT DAYS 

——  HINDI SHAYARI

——  KAVITA  HINDI ME 

—— 12TH (ARTS) BIHAR BOARD

*****************************************

 गणित : –   दैनिक जीवन में प्रयोग 

गणित  महत्वपूर्ण विषयों में से एक है जिसे हम  दैनिक जीवन में प्रयोग करते  है। घर हो या दुकान, वर्षा , तापमान, गति, वजन इत्यदि  सब जगह गणित है।   यदि  नौकरी चाहते  है, चाहे आप पायलट, इंजीनियर, डॉक्टर या प्रोफेसर बनना चाहते हों, गणित की हमेशा आवश्यकता होती है। यहाँ मै Class 10th Maths Solution in Hindi विषय पर विस्तार रूप से चर्चा करेंगे।

मेरा मानना ​​है कि यह सबसे दिलचस्प विषयों में से एक है। जब मैं एक छात्र था तो मैं गणित से निपटने का आनंद लेता था क्योंकि गणित में उसके तथ्य को समझना और सूत्रों को सही तरीके से प्रायोग  करना हम सिखाते है। Class 10th Maths Solution in Hindi,  गणित में कुछ भी ऐसा नहीं है जिसे मुझे कुछ सूत्रों से अलग याद रखना पड़ता है।

आज हम गणित के कुछ मूल विषयों के बारे में जानेंगे जो आपकी पढ़ाई में मदद करने वाले हैं। जिन विषयों पर चर्चा होने वाली है, उन्हें समझना बहुत आसान है और इससे आपको गणित की सही नींव रखने में मदद मिल सकती है।

10th Class Maths Solution in Hindi  yahan hamlog Class Tenth ke Ganit ke sath sath sabhi vishyo ko dekhenge jiska Link niche hai.

• संख्या( Numbers )—अंको के समूह को संख्या कहते हैं या ऐसे भी कह सकते हैं कि दो या दो से अधिक अंकों के समूह को नंबर या संख्या कहते हैं।

जैसे-15, 18, 49, 45 यह संख्याएं हैं किंतु एक 7, 8, 9 यह सभी अंक है

Kinds of  Numbers (संख्या के प्रकार)

• प्राकृतिक संख्या (Natural numbers) — गिनती की संख्या को प्राकृतिक संख्या यानी नेचुरल नंबर कहते हैं

जैसे 1, 2, 3, 4 ,5… ……………..

• पूर्ण संख्याएं (Whole numbers) —शून्य सहित प्राकृत संख्याओं  (Natural numbers) के समूह को पूर्ण संख्याएं कहते हैं

जैसे 0, 1, 2, 3, 4, 5 ……………..

• पूर्णांक संख्याएं (Integer numbers)—-पूर्ण संख्याएं  (Whole numbers) और उसके ऋणात्मक से बने समूह को पूर्णांक संख्या कहते हैं

जैसे–………………………. – 3, – 2, – 1,  0, 1, 2, 3 ……………….

• सम संख्याएं  (Even numbers) —  वे संख्याएं जो 2 से पूर्णतः  विभाजित हो जाए उसे  Even numbers कहते है।

जैसे—  2,  4,  6,  8, —————–

• विषम संख्याएं  (Odd numbers)—-वे संख्याएं जो 2 से पूर्णतः  विभाजित ना हो  उसे  Even numbers कहते है।

जैसे—  3 , 5 , 7, 9 , —————–

• अभाज्य संख्याएं (Prime numbers)—  जो संख्या एक और खुद से विभाजित हो कोई दूसरे संख्या से विभाजित ना हो Prime numbers  कहलाते हैं

जैसे —  2,  3,  5,  7,  11,  13,  17 ——————–

• भाज्य संख्याएं  (Compound numbers) —– वे संख्याए जो  कम से कम तीन और अधिक संख्याओं से विभाजित होती है.

जैसे 4, 6, 8 —————

4 — 1 ,2 ,4

6 —1, 2, 3, 6

8– 1,2,4,8

• परिमेय संख्याएं (Rational numbers)—- वह संख्या जिसे अंश / हर के यानी p/q के रूप में व्यक्त कर सकें जहां q  का मान शुन्य  नहीं  हो.

जैसे — 4/5, 7/2, 94/7, 45, 89 —————

•  अपरिमेय संख्या (Irrational number)— वह संख्या जिसे अंश / हर के यानी p/q के रूप में व्यक्त नहीं किया जा सकता है.

संख्या को दो भागों में बांट सकते हैं

•  वास्तविक संख्या (Real number) —-वह संख्या जो वास्तव में वह हो

इसके अंतर्गत आते हैं — सम संख्या,  विषम संख्या,  पूर्ण संख्या,  पूर्णांक संख्या,  परिमेय संख्या,  अपरिमेय संख्या,  प्राकृत संख्या,  दशमलव संख्या,  अभाज्य संख्या,  भाज्य संख्या इत्यादि

• काल्पनिक संख्या (Imaginary number) — वह संख्या जिसकी हम सिर्फ कल्पना कर सकते हैं

ऋणात्मक संख्याओं का वर्गमूल ज्ञात  नहीं कर सकते हैं इसकी हम कल्पना मात्र कर सकते हैं यदि कोई संख्या रूट के अंदर हो और उसमें घटाओ का निशान लगा हो तो वह काल्पनिक संख्या के अंतर्गत आते हैं

जैसे

Class 10th Maths Solution in Hindi

Real Number

Any number which you can think about is a real number. The numbers that exist and which can be calculated can be termed as real numbers. For example, 1, 34, -3, 0.34, -1.456, 5/4, etc.

Polynomials

‘Many terms’ is the meaning of polynomials, where ‘poly’ refers to ‘many’ and ‘nomial’ refers to terms. Polynomials refer to constants (like 1, 3, 5, etc.), exponents (like 3^2, 4^5, 6^9, etc., where 2, 5, 9 are the exponents), and variables (like x, y, z, etc.).

The exponents of a polynomial cannot be zero, and a polynomial does not allow a variable to divide any number.

Polynomials are mostly classified into three forms:-

• Monomial: – Expression with a single term falls under monomial. .
• Binomial: – Expression with two terms is termed as binomial. .
• Trinomial: – Expression consisting of three terms is known as trinomial.

In this post we study redarding Class 10th ncert maths  solution

Pair of linear equations in two variables

Those equations which can be represented in the form ax + by + c = 0, where a, b, c are a real number, are known as a linear equation in two variables.

Example: –

Given equation, 3x + 4y = 11 (where x and y are the variables)

Now if we substitute x with 1 and y with 2, then the equation is as followed.

3(1) + 4(2)

= 3 + 8

= 11

Since we have obtained the conclusion of L.H.S. = R.H.S.

Hence we can conclude that the values of x and y are 1 and 2.

Exception: –

Suppose we have added some other values of x and y. Let us assume x = 2 and y = 4.

Therefore we have,

3(2) + 4(4)

= 6 + 16

= 22

Since L.H.S. is not equal to R.H.S., hence we can say that the values of x and y being 2 and 4 cannot be the solution of the equation 3x + 4y = 11. You can get information about 10th class math book solution in Hondi. 

Quadratic Equations

A quadratic equation is an equation which consists of a degree of 2. The term ‘quad’ means square since every quadratic equation consists power of 2 in it.

Standard form of the quadratic equation: –

a(x^2) + bx + c = 0, where a, b, c are real numbers and the value of a can never be equal to zero. In the equation 2(x^2) + 4x – 2 = 0, the values of a, b and c are 2, 4 and -2.

If you are from Bihar And Uttar Pradesh and searching on internet Class 10th Maths Solution in Hindi . Here we provide you Mathematiecs  in video formate in Hindi.

Some more examples of quadratic equation: –

• (x^2) + 3 = 0, here the value of a, b and c are 1, 0 and 3
• 2(x^2) – 4x = 0, the values of a, b and c are 2, -4 and 0

The equation, x + 4 = 0 cannot be a quadratic equation, since the constant of (x^2) can never be zero.

Rules for solving quadratic equations: –

• Using factorization

Suppose the given equation is (x^2) + 3x + 2

Then the method for solving this is as follows

Step 1:- (x^2) + 2x + x + 2 [break the equation in such a manner such that when we add ax + bx, we get cx, where a, b, c are a real number, also look that when we multiply a with b, we get c]

Step 2: – x(x +2) + 1(x+2) [Take common from first and second term and common from third and fourth term]

Step 3: – (x+2) (x+1) [take (x + 2) common and then write the remaining term together]

• Sridaracharya Method

To find the value of x just put the values of a, b, and c in the following formula.

x = (-b +- {(b^2) – 4ac}^1/2)/2a [generally two values will be derived for x, and both the values will be satisfying the given set of the equation]

Arithmetic Progression

Arithmetic Progression which is also known as A.P. is a set of numbers which has a constant difference between the first and second number.

Example: –

2, 4, 6, 8, 10, 12, 14, 16, etc.

In the above set, the difference between every first and second number is 2, hence it can be termed as an Arithmetic Progression. The common difference in Arithmetic Progression can be found by subtracting the first number by the second one.

यदि आप वर्ग दशम के छत्र है और यह सर्च कर रहे है  Class 10th Maths Solution in Hindi तो आप सही जगह पर आ चुके जहा आप लोग गणित के विषय में विस्तार से देखेंगे

Triangles

Triangle is a closed figure which has three line segments. It is a polygon of three sides.

Example: –

 

Properties: –

• There are three vertices (corner of the triangle) in a triangle
• The line segment which is present at the bottom side can be termed as the base of the triangle
• The altitude is the distance from the base to the opposite side of it
• There are three medians (the line from the vertex to the midpoint) in a triangle and these three intersect each other at a particular point

Types of Triangles: –

The different types of triangles are as follows.

Isosceles: – Triangle with two equal sides is known as an isosceles triangle.

Equilateral: – In this triangle, all three sides are equal.

Scalene: – All the three different sides are of different length.

Right Angle: – A triangle whose one side has an interior angle of 90 degrees is known as a right-angle triangle.

Obtuse: – The triangle whose one of the interior angle is greater than 90 degrees is known as the obtuse angle.

Acute: – The triangle where all the three interior angles are less than 90 degrees is known as the acute angle.

Equiangular: – Triangle which has equal interior angles is known as an equiangular triangle.

यदि आप वर्ग दशम के छत्र है और यह सर्च कर रहे है  Class 10th Maths Solution in Hindi step by step.

Co-ordinate Geometry

Before understanding the concept of co-ordinate geometry, let us understand a plane. A plane is a flat surface which can move infinitely towards any direction. Now while locating a particular point on a plane, you just need to figure out the coordinates. Now the coordinate geometry is to help you while locating a particular point on a plane.

A branch of geometry which allows us to figure out the coordinates and locate it in a plane is known as coordinate geometry.

Example: –

Let us say the value of x and y is 1 and 2, therefore the representation of the number in a plane will be as the figure below.

 

 

The above figure gives the idea of how a particular point can be located in the plane with the help of coordinates of x and y. If the value of x is positive then we need to locate it on the right side of X-axis, and if negative then it will be located on the left side of X-axis. Similarly, for a negative value for y, we will locate in the lower part, while for a positive value it will be located in the upper part.

Here we study  Class 10th Maths Solution in Hindi very easily.

Trigonometric ratio and identities

Trigonometry is one of the parts of the mathematics which most of the students find difficult. But it can be easily taken down once someone looks over the formulas. Just like the formula of (a + b) ^2 = (a^2) + (b^2) + 2ab, trigonometry has its own set of formulas. Just like the algebraic notation, trigonometry can be written down in similar notations.

The following are the important formula while talking about trigonometry relations which relates trigonometric ratios and identities.

• sin0 = 1 / cosec0
• cos0 = 1 / sec0
• tan0 = 1 / cot0
• tan0 = sin0 / cos0
• cot0 = cos0 / sin0

While talking about the trigonometric ratio, it can only be applied for right-angle triangle since once angle has to be 90 degrees for a trigonometry ratio. It generally involves hypotenuses, perpendicular and base.

The formulas for trigonometry ratio are as follows.

• sin0 = perpendicular / hypotenuse
• cos0 = base / hypotenuse
• tan0 = perpendicular / base
• cosec0 = hypotenuse / perpendicular
• sec0 = hypotenuse / base
• cot0 = base / perpendicular

Generally, you can use the following sentence for remembering the above formulas, “Some People Have Curly Brown Hair Turn Permanently Black”. Here ‘s’ stands for sin, ‘p’ for perpendicular, ‘h’ for the hypotenuse, ‘c’ for cos, ‘b’ for brown, ‘h’ hair, ‘t’ for a  tan, ‘p’ again for perpendicular, and similarly ‘b’ for black. Regarding the cosec, tan, and cot you only need to reverse the formula of sin, cos, and tan.

Some applications of trigonometry

Trigonometry helps us to find out the height and distance which can be done without even actually measuring it.

All we need is to understand some basic concepts for calculating the height and distance of an object. Some of the basic elements are as follows: –

Line of sight: – It is the imaginary line which is created through our eyes when we look over a particular object.

Horizontal Line: – It is the distance obtained between the person and the object.

The angle of elevation: – It is the angle made by the line of sight and the horizontal line. It is generally obtained when we look over any object in an upward direction.

 

 

The angle of Depression: – It is the angle formed when a person has to look downwards.

 

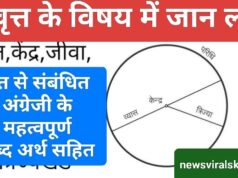
Circle

A circle is a shape which is closed from all the points and the distance from the center to any point is equal.

Some formulas of circle: –

Area = (22 / 7) * (radius ^ 2)

Circumference = 2 * (22 / 7) * radius

Diameter = radius / 2

 

 

Areas related to circle

We already know the formula for the area of the circle and the circumference. Similarly, the various other formulas are as follows.

Area of semicircle = { ( 22 / 7 ) * radius * radius } / 2

 

Area of a quadrant = { ( 22 / 7 ) * radius * radius } / 4

Area of the minor sector: – The area which lies between two radiuses is known as the area of the sector.

 

Area of minor sector = (a / 360) * (22 / 7) * (radius ^ 2)

Area of major sector = { (360 – a) / 360 } * (22 / 7) * (radius ^ 2)

Area of segment = area of sector – area of the triangle

= (radius ^ 2) [(((22 / 7) * a) / 360) – ((sin a / 2) * (cos a / 2))]

Construction

The task of drawing a particular shape like circle, triangle, lines, etc. with the help of the equipment like (compass, straight-edge, etc.) is known as construction. Construction helps us to understand the concept of geometry; it also helps in drawing shapes which cannot be drawn normally through measurements.

Surface areas and volume

Surface area of cuboid = 2(lb + bh + hl), where ‘h’ stands for height, ‘l’ for length, and ‘b’ for breadth.

Surface area of cube = 6 * (side ^ 2)

Curved surface area of a cylinder = 2 * (22 / 7) * radius * height

Total surface area of cylinder = (2 * radius * (22 / 7)) (radius + height)

Curved surface area of a cone = (22 / 7) * radius * length

Total surface area of cone = ((22 / 7) * radius) (length + radius)

Surface area of a sphere = 4 * (22 / 7) * (radius ^ 2)

Curved surface area of a hemisphere = 2 * (22 / 7) * (radius ^ 2)

Total surface area of a hemisphere = 3 * (22 / 7) * (radius ^ 2)

Volume of cuboid = length * breadth * height

Volume of cube = edge ^ 3

Volume of cylinder = (22 / 7) * (radius ^ 2) * height

Volume of a cone = (1 / 3) * (22 / 7) * (radius ^ 2) * height

Volume of the sphere = (4 / 3) * (22 / 7) (radius ^ 3)

Volume of the hemisphere = (2 / 3) * (22 / 7) * (radius ^ 3)

बहुत पहले से सोच रहा था कि हमलोग  Class 10th Maths Solution in Hindi विषय पर बातचीत करे वह दिन हमारे सामने है।

Statistics

When raw information is collected for a specific purpose, then it is termed as data. The study which gives us the idea of dealing with the analysis of the data, it is known as statistics.  Bar graphs, histograms, and frequency allow us to represent data graphically. Following are terms you will encounter in statistics. Class 10th Maths Solution in Hindi

Mean: – It the average of the set of values. Mean = (sum of all observation) / number of observation

Median: – It is the middle point of the number of a set of values. Median = (n + 1) / 2, where ‘n’ is the number of observations.

Mode: – The most frequently occurring observation is termed as a mode.

Probability

It is the chances of sudden activity. For example, when a coin is tossed, there is a probability of 50-50 to get a head as well as a tail.

P (E) = (number of trials in which the event occurred) / (total number of trials), where P (E) is the probability of an event.

Conclusion

Mathematics has always been one of the most important subjects in every student life. The above-mentioned topics are the ones which helps you to build a proper foundation and which is also going to be used when you go for a deeper study. Class 10th Maths Solution in Hindi

Also read– social science